Consecu-doku is a variant of classic Sudoku. It still involves rows,
columns, and
mini-boxes and as usual, digits 1 through 9 must exist in all of them
without conflict.
Unlike classic Sudoku, Consecu-doku grids contain circles between some adjacent
cells. Those circles indicate that the numbers in those cells must be
consecutive
(ascending or descending).
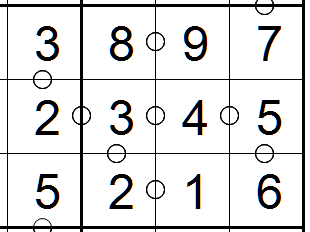
Also, the numbers in adjacent cells that do not have a circle CANNOT be consecutive.
These puzzles can be solved using the typical Sudoku solving techniques (ie. hidden
singles, naked singles, hidden doubles, triples, etc). They can be solved without
resorting to advanced strategies such as X-wings, XY-Wings ,Swordfish, etc.
Consecu-doku puzzles can have as few as one "given" digit. Despite the low number
of given digits, there is only one solution to each puzzle. I have gone to great lengths
to ensure that every puzzle is valid (ie. one solution only).
For this tutorial, adjacent cells are referred to as consecutive or nonconsecutive cells
depending on the presences or absence of circles.
Here are a few tips to get you started:
Tip #1 Look at solved cells and "givens"
Cells adjacent to solved or given cells will eliminate candidates as shown here:
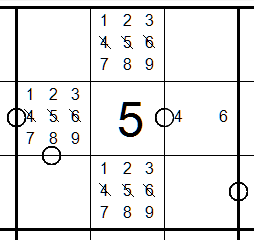
The cell to the right of the 5 can only be a 4 or 6.
The cell to the left of the 5 cannot be a 4 or 6 (or of course 5).
Tip #2 Look for cells with 2 circles
Cells with two circles on opposite sides cannot contain a 1 or a 9
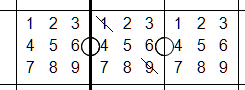
The digit 1 can only be consecutive with digit 2. Since it is not possible to have
two 2's in the same row, digit 1 is not possible in the center cell. Similarly, digit
9 can only be consecutive with digit 8. So 1's and 9's are not possible in cells
with two opposite circles.
When a cell has two circles not opposite to each other ("L" shaped), these cells
also cannot be 1 or 9 if the cells reside in the same box).
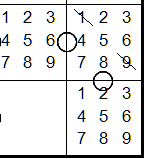
In the example below, the three adjacent cells do not reside in the same box.
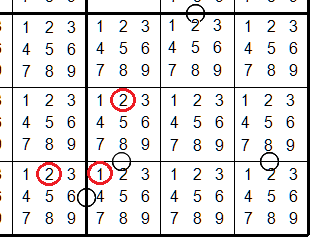
In this case 1's and 9's are still possible.
Tip #3 Look for consecutive cells that form long chains
These can be very helpful. But be careful when the chain
enters a new box as the direction can change!
Tip #4 Look for cells that are missing 2's or 8's
When a cell is missing a 2, adjacent cells with circles
cannot contain a 1
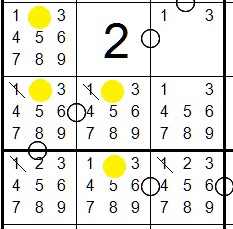
Cells with missing 8's will remove 9's from adjacent cells with circles
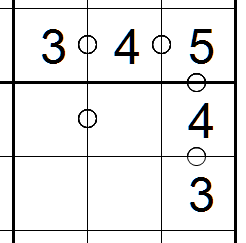
Tip #5 "Min - 1 and Max + 1 rules"
The minimum value of a cell is the minimum - 1 value of
a consecutive cell. For example, the minimum value in
the center cell is 5. The minimum value in any consectuve
cells is 4. Values below 4 can be eliminated.
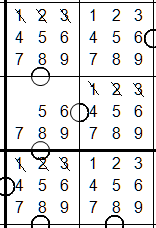
The maximum value of a cell is the maximum +1 of a
consecutive cell. In this example, the maximum value
of the center cell is 4. The maximum value of the consecutive
cells is 5. Values above 5 can be removed.
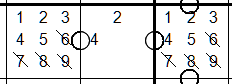
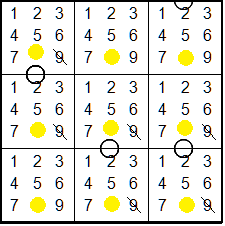
Tip #6 Look for bivalue cells with consecutive values
Bivalue cells have only two candidates remaining. If they are consecutive,
they will eliminate those candidates from non-consecutive cells.
The pair in the center cell (45) are consecutive which allows removal of
those candidates from non-consecutive cells. Also note how the pair
affects the consecutive cell to the left. The candidates in that cell must be
within -1 below or +1 above the pair (3456) , otherwise they are eliminated.
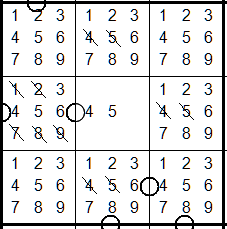
Tip #7 Consecutive Trips
A cell with three consecutive digits affects neighboring non-consecutive cells.
The middle digit (5 in this case) cannot be present in those cells.
Tip #8 Bivalue cells where difference = 2
Just like the consecutive trips, bivalue cells with a difference of 2
(ie. 13, 57, 46, etc), allows removal of the missing middle digit
(5 in this case).
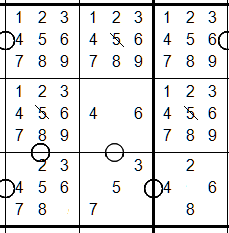
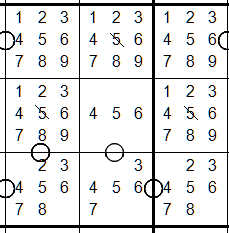
Tip #9 Think "parity" (ie. even or odd)
Consecutive cells must have opposite parity. If all candidates in a cell are odd,
candidates in consecutive cells must be even (and vice versa)
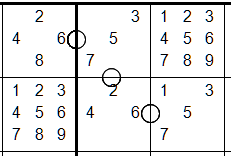
Note how the candidates alternate between even and odd in consecutive cells.
Tip #10 Hidden singles and Locked Candidates are common
Whenever you are able to eliminate a candidate, check the related
houses (row, column, box) for hidden singles and locked candidates.
This is the same as in classic sudoku but they are more common in
Consecu-doku.
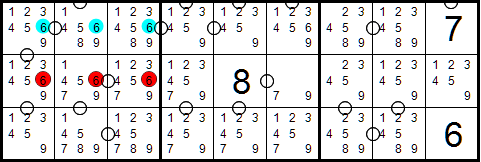
What are locked candidates? (this is from classic sudoku)
Locked Candidates: The red 6's are confined to the middle row
therefore they cannot exist anywhere else in the box. The blue
6's can be removed.
Similarly these red 3's are confined to the box therefore they
cannot exist anywhere else in the row. The blue 3 can be
removed.
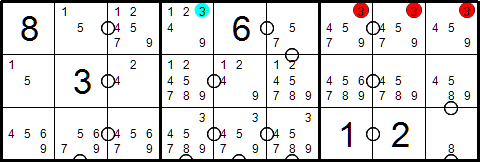
Tip #11 Avoid the Deadly Pattern Strategies
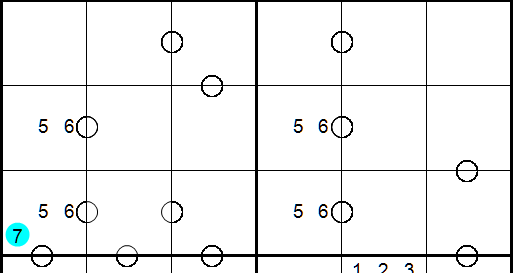
There are a handful of advanced sudoku solving techniques that
are based on avoiding multi-solution situations. These include UR's
(Unique Rectangles, Hidden Rectangles, Deadly Patterns, BUG +1
etc). In classic sudoku, removing the blue 7 would create a deadly
pattern which would allow for two different solutions. Therefore 7
would be the correct solution for that cell. However, in consecu-doku,
the consecutive / non-consecutive rules can allow removing the blue 7 and
still have one unique solution for the puzzle. Do not use UR strategies
in consecu-doku!
I hope you enjoy this book and these puzzles. I welcome questions,
comments, criticisms, yada yada so feel free to drop me an email at:
jumpindoc@gmail.com
And please check out my web site at:
www.manifestmaster.com
Enjoy!
"Doc" John Musgrave
















