By John Musgrave
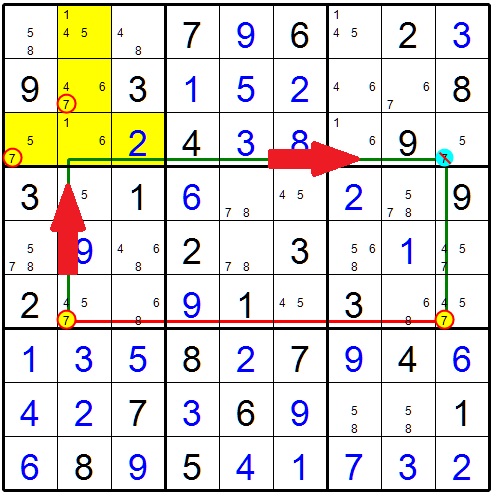
Figure 1
This is definitely a technique worth learning! Empty Rectangles are common and relatively easy to locate. An empty rectangle will only eliminate one candidate but this could be enough to break a log jam.
Sadly the name Empty Rectangle is not very descriptive. As figure 1 shows, the strategy is rectangular in shape. That rectangle has nothing to do with the name of the strategy. Very confusing! I wish it had a better name. But I digress………..
So what is an empty rectangle?
The Empty Rectangle is a sudoku solving technique that takes advantage of a phenomenon called the Hinge. A hinge allows the influence of a candidate to make a 90 degree turn as shown in figure 1.
The Empty Rectangle technique will always follow just one candidate. There are three components used in this technique:
The key is the conjugate pair. In figure 1, this is the pair of 7’s in row 6. Whichever 7 is true in row 6, the blue 7 in row 3 column 9 will be eliminated.
So there is an Empty Rectangle and a Hinge. What do they mean? In a given box, if you pick one row and one column, the four remaining cells will form a rectangle (or square). The selected row and column form a “hinge” (shown in yellow in figure 2). Empty Rectangle means that the candidate of interest is not present in any of the white cells. Those white cells can be givens, solved cells, or unsolved cells with one or more possible candidates. But again, the candidate of interest is not present in any white cell. This allows the influence of a candidate to make a 90 degree turn.
|
|
|
|
|
|
|
|
|
|
|
|
Figure 2 Hinges
Figure 2 shows the nine possible configurations of an empty rectangle in a 3x3 box. The white cells represent the rectangle. If the candidate of interest is not present in any of the white cells, the rectangle is said to be “empty”.
Since the candidate is not present in any of the four white cells, it must be present somewhere in the yellow cells. If it is present in only one of the yellow cells, you have identified a single for that box and can move on. If the candidate is present 2 or 3 times, they must not be located in the same row or same column (if they were, that would be a locked candidate which would eliminate either the target cell or one of the conjugate pair candidates). In order to form a hinge, the candidate must be present at least once in the yellow row and yellow common (and not just in the intersection of the row and column).
The concept of bands and stacks is important here. Remember that a band is three boxes arranged horizontally. A stack is three boxes arranged vertically. There are three possible bands and three possible stacks.
|
|
|
|
|
|
|
|
Figure 3 Horizontal bands and vertical stacks
Searching for an Empty Rectangle is as follows:
In this example, we will look for a conjugate pair in a row. Obviously the same strategy applies to a conjugate pair that resides in a column. In figure 4, there are multiple conjugate pairs. For this example, we will focus on the 9’s in row 7. There are only two 9’s in row 7 so they are strongly linked (note that this pair is located in the bottom horizontal band).
Figure 4 - Conjugate pair of 9’s in row 7
Target cells are cells where candidate elimination will occur. For each empty rectangle, there will only be one cell where a candidate is eliminated. There are twelve possible locations for target cells. Note the horizontal band where the conjugate pair is located. Target cells are located in the other two horizontal bands.
Figure 5 shows the location of the twelve possible target cells. Those are the cells in the same columns as the conjugate pair. In this case, that will be rows 1 through 6. Rows 8 and 9 reside in the same horizontal band as the conjugate pair and can be ignored.
Figure 5 - Three potential target cells (green)
Figure 5 shows that there are three target cells that contain a 9 (shown in green). These are the potential target cells. For each target cell, we must look for a matching hinge.
Figure 6 - Target cell in row 1 column1 (bad)
The first possible target cell is the 9 in row 1 column 1. To look for a hinge, we search in the box defined by the target cell row (row 1) and the opposite column (column 7). In this case, it is box 3 (see figure 6). By coloring the row and column, the four remaining white cells create the rectangle (or square in this case). Our candidate 9 is present in two of the white cells. Therefore the rectangle is not empty and we can move to the next target cell.
The next target cell is the 9 in row 1 column 7. The hinge box will be the box in row 1 and the opposite column (column 1). Box 1 is the potential hinge box. After highlighting the involved row and column, it is apparent that there are no 9’s in the four white cells. WE HAVE AN EMPTY RECTANGLE! Success! The hinge works and now the 9 in the target cell (row 1 column 7) can be removed.
Figure 7 - Target cell row 1 column 7 (good!)
For completeness sake, let’s check out the remaining target cell in row 3 column 1.
Figure 8 Target cell row 3 column 1 (bad)
In figure 8, the target cell is the 9 in row 3 column 1. The possible empty rectangle will be in box 3. After highlighting the row and column, it is apparent that the white rectangle is not empty (two 9’s present).
OK, it’s your turn. Figure 9 shows a partially completed sudoku puzzle. There are two empty rectangles present. Can you find them? (there are hints and answers at the end of this text)
Figure 9 - Find the empty rectangle
Figure 10 - Find the empty rectangle
So the steps in finding an Empty Rectangle are:
I hope you find this text helpful. I welcome your comments, questions, suggestions, and criticisms.
Happy puzzling!
Doc John
HInts:
For figure 9, look for a conjugate pair of 3’s
For figure 10, look for a conjugate pair of 5’s
Figure 9 answers:
Conjugate pair of 3’s in row 1
Conjugate pair of 3’s in column 2
Figure 10 Empty Rectangles
Conjugate pair of 5’s in row 7
Conjugate pair of 5’s in row 7