Sudoku
Using Brute Force
(a vb.net project)
By John Musgrave
(The brute force source code can be found in the BruteForce.zip file)
BRUTE FORCE is a method of solving a sudoku puzzle. It is nothing more than an organized trial and error until the puzzle is solved or proven unsolvable. For most puzzles solvers (ie. humans) It is only practical as a solving strategy when there are very few unsolved cells left in a puzzle. Using brute force at the beginning of most puzzles will involve thousands (sometimes millions) of steps.
The code presented here was written using vb.net. However the logic presented in this text can be applied to any programming language. I am using vb.net for this project, specifically Microsoft Visual Studio Community 2017 version 15.9.11 (which can be downloaded for free).
In this text and in the attached code, you will find that I am guilty of anthropomorphism which is applying human characteristics to non_ human objects. Phrases like a method wants to do something or a cell can see a number or a subroute tries to do something are examples of this. Forgive me for my sins but I find that this can be a clear way to explain a procedure. That’s just me.
The brute force algorithm is designed to:
The brute force method in this code module reads the cells from left to right and top to bottom. The numbers already present are the puzzles “givens”. The method begins by finding the first empty cell (non given) in the grid. At that point, it enters the brute force loop which is as follows:
These three steps are placed in a Do/Loop. It continues to loop until puzzle validity is either proven or disproven.
If a sudoku puzzle is unsolvable (ie. no possible solution), brute force will eventually backtrack to the first non-given cell in the puzzle and find that it has no possible value. This proves that the puzzle has no possible solution. (The exception to this is an invalid puzzle with conflicting givens, more on this later).
When the brute force routine successfully places a non conflicting value in the last non given cell, a solution to the puzzle has been found. The puzzle has been proven to be solvable. However this does not yet rule out multiple solutions.
Once a solution has been found, brute force preserves all of the current values in the grid and returns to the last non given cell in the grid. That cell’s value is incremented and the process continues. If it backtracks to the first non given cell in the grid and cannot find a valid value for it, it proves definitively that no other solutions exist. Conversely if it returns to the last non given cell in the grid and successfully places a non conflicting value in it, a second solution has been found and validity is disproven.
This method has the somewhat dubious quality of being able to find all of the possible solutions to an invalid puzzle. Most applications are content to exit after detecting a second solution once validity has been disproven. However, for the more curious sudoku explorers, the option to quantitate the number of available solutions can be useful (or at least interesting). Limits need to be placed on this method since an invalid puzzle can have millions of solutions.
Writing code that implements the brute force method can be challenging. It is important that the algorithm has as few steps as possible. It will execute thousands (if not millions) of trials. The algorithm involved can either be recursive (ie. a method that calls itself) or use nested loops. This author has encountered many “OUT OF STACK SPACE“ errors when using recursion to perform brute force. Apparently other authors have been quite successful using recursion and I bow to their expertise. However in this project I use nested loops. The brute force subroutine is shown below (as well as in the attached code module). The user supplies the sudoku puzzle in an 81 character string and BruteForce returns a Solutions() array. Examining the Solutions() array will determine the status of the puzzle.
If the Solutions() array has more than one element, the puzzle has multiple solutions. If the Solutions array has only one element and Solutions(0) = Nothing, then the puzzle is invalid (no possible solution). When the Solutions() array has only one element and Solutions(0) is an 81 digit string, the sudoku puzzle is valid and has one unique solution.
The puzzle format in Sub BruteForce() is an 81 character string which is supplied by the calling method. Numeric characters in the string are the puzzle’s “givens”. Empty cells can be zero or any non-numeric character.
The puzzle string is read into a two dimensional array called Cell(row,col).
I am certain to be criticized for dimensioning the Cell() array by using Dim Cell(9,9) instead of Dim Cell(8,8). By including the zero element in the array, Cell(8,8) is an 81 element array while Cell(9,9) has 100 elements, 19 of which are ignored. I find it more intuitive to refer to rows and columns as 1 through 9 rather than 0 through 8. Shoot me.
Keeping track of “givens”.
When focus is moved to a new cell, it needs to know whether or not that cell is a given. Obviously a Cell(row,col) value of zero would not be a given. However the values in the Cell() array will change as the method progresses. There needs to be a way to determine whether or not a non zero cell is a given. This can be done in several ways. One method would be to create a parallel boolean array such as:
Dim Given(9,9) as boolean
All of the given cells would be set to TRUE and the unknowns would be FALSE. This would work ok but there is a better way.
Another possibility would be to refer to the original 81 character string. An element the the Cell(row,col) array can find its position in the puzzle string from this formula:
Position = ((row - 1) * 9) + col
So a function call like this could be used to detect givens.
If IsGiven(row,col) = False then
‘Do something
End if
|
Function IsGiven(row As Byte, col As Byte, Puzzle as string) as boolean
Dim Position as Int16 IsGiven = False
Position = ((row - 1) * 9) + col If Val(Mid(Puzzle,Position,1)) <> 0 then IsGiven = True End if
End Function
|
Both methods described above work well. However, I decided on a different method. Rather than creating a separate array or new function, givens as assigned negative values in the Cell() array. The Cell() array is created as variable type SByte as follows:
Dim Cell(9,9) as SByte
SByte indicates a signed byte (values -128 to +127). (Byte is 0 to 255). Since the SByte data type allows for negative values, it is more appropriate for the Cell() array . The array is created by reading the 81 character puzzle string. This code populates the Cell() array where all givens are negative. It reads the puzzle string one character at a time and populates the Cell() array.
|
Dim Cell(9, 9) As SByte
For Row = 1 To 9 For Col = 1 To 9 x = x + 1 Cell(Row, Col) = Val(Mid(Puzzle, x, 1)) * (-1) Next Col Next Row
|
Detecting the givens is then as simple as:
If Cell(row,col) > -1 then
‘Not a given, do something
End if
Here is the entire brute force subroutine (also see the ModBruteForce.vb module)
.
|
Sub BruteForce(ByRef Puzzle As String, ByRef Solutions() As String)
‘Don’t forget the ByRef for the Solutions() array
Dim Row As Byte = 1 Dim Col As Byte = 0 Dim x As Byte = 0
Dim DeadEnd As Boolean = False Dim NewSolution As String Dim SolutionCounter As Int16
Dim Cell(9, 9) As SByte 'SByte because givens are negative.
'Populate the Cell() array from the puzzle string. For Row = 1 To 9 For Col = 1 To 9 x = x + 1 Cell(Row, Col) = Val(Mid(Puzzle, x, 1)) * (-1) Next Col Next Row
'find first empty cell in grid Row = 1 Col = 0 'Col will be incremented in the next line Call MoveToNextCell(Row, Col, Cell) ‘find non given cell
Do 'Handle current cell Do 'increment cell's value Cell(Row, Col) = Cell(Row, Col) + 1 If Cell(Row, Col) > 9 Then ‘need to backtrack Cell(Row, Col) = 0 DeadEnd = True 'tells routine to backtrack Exit Do End If Loop While HasConflict(Row, Col, Cell)
'move to next cell (forward or backtracking) If DeadEnd Then 'need to backtrack to previous cell Call MoveToPreviousCell(Row, Col, Cell) DeadEnd = False If Row = 0 Then 'Done, no more solutions 'The solutions() array is returned Exit Do 'exit the loop and the subroutine End If Else Call MoveToNextCell(Row, Col, Cell) If Row > 9 Then 'found a solution SolutionCounter = SolutionCounter + 1
'save in Solutions() array NewSolution = CreateSolutionString(Cell) Call SaveSolution(NewSolution, Solutions)
Select Case SolutionCounter 'Exit or continue? Case 1 'Found a solution 'return to the last non given cell Call FindLastNonGivenCell(Row, Col, Cell) Case 2 'Found two solutions 'In Solutions() array Exit Do Case Else 'This could be used if need to count number of solutions in an invalid puzzle End Select
End If End If Loop
|
When the brute force routine is evaluating a cell, all previous cells in the grid are non zero. They are either givens (negative) or have been assigned a value (positive). All remaining cells (past the current cell) are either zero or negative.
As a result, there is an important difference between moving to the next available cell versus backtracking to a previous cell. When a cell is successfully assigned a value (without conflict), the focus is moved to the next empty cell. The new cell’s value is zero. Its value is incremented until a non conflicting value is found. If a non conflicting value cannot be found, the cell is blanked (set to zero) and brute force must then backtrack to the previous non-given cell and increment its value. That cell’s value is incremented starting at its current value, not zero. If all possible values cause conflict, this cell is blanked and brute force backtracks again to a previous non-given cell. When backtracking, the algorithm only tests for values greater than the cell’s original value (ie. the cell’s value when focus moves to that cell).
In a nutshell, here is what the Sub BruteForce() method will do:
When a valid puzzle string (ie. one unique solution) is presented to this subroutine, it will work its way to the last non given cell in the puzzle grid and assign it a non conflicting value. At that point it will create an 81 character string from the Cell() array and save it in the Solutions() array. Focus then returns to the last non given cell in the Cell() array. Its value is incremented (or attempts to) and the algorithm continues. Eventually the method will backtrack to the first non given cell in the puzzle and find that it has no possible value. At that point, the method exits and the Solutions() array is returned to the calling method.
When a solution is found, all elements in the Cell() array are non zero. The subroutine MoveToNextEmptyCell() will return row = 10. This indicates that the last non given cell in the puzzle has successfully been assigned as value. The Cell() array now represents a solution to the puzzle. That solution is stored in the Solutions() array as an 81 character string. The focus then moves to the last non given cell in the puzzle in order to search for another possible solution.
The attached code contains two brute force methods. They are:
Sub BruteForce()
Sub BruteForceEnhanced()
The first method is shown to demonstrate the simplistic nature of the brute force algorithm. Although it accomplishes the task well, there are opportunities to enhance the algorithm to make it more efficient. These are present in the latter method and include:
These enhancements are shown in the code module in Sub BruteForceEnhanced(). They involve adding code before entering the main Do/Loop.
If the puzzle string is 81 digits with no zeros (ie. a solved puzzle already), brute force will encounter an error before entering the main loop. It is searching for the first available empty cell. Since it can’t find one, it will attempt to search in row 10 which doesn’t exist. When this happens, the user will receive this error message:
System.IndexOutOfRangeException: 'Index was outside the bounds of the array.'
This can be easily avoided by adding this code before entering the main DO/LOOP.
If Row > 9 Then
'string is all givens - found a solution
Solutions(0) = Puzzle
Exit Sub
End If
Conflicting Givens
Checking for conflicting givens is more involved. In fact, doing this is critical! The brute force algorithm itself does not check for conflicting givens. Consider this obviously invalid puzzle:
The brute force subroutine will find a single solution and call this a valid puzzle. It will find non conflicting values for all of the empty cells.
Fortunately, detecting conflicting givens is a simple task. A function has been created called Function GivensConflict(Cell) (see code module for this function)
Placing this code before entering the main Do/Loop will return an empty Solutions() array to the calling routine where Solutions(0) = Nothing.
If GivensConflict(Cell) Then
ReDim Solutions(0) 'equals nothing
Exit Sub
End If
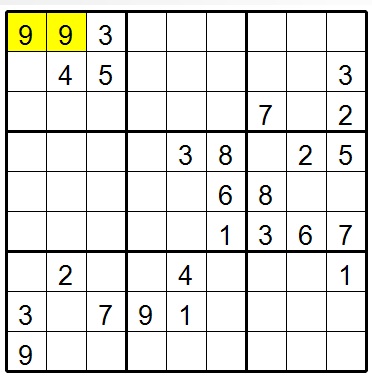
Another obviously invalid puzzle is one with fewer than 17 givens. Mathematicians much wiser that this author have determined that a valid sudoku puzzle must have at least 17 givens. For completeness sake, this situation is not necessarily a multisolution situation. A puzzle with only 9 givens can have no possible solution. In this figure the cell shown in yellow has no possible value.
The brute force routine can handle puzzles with fewer than 17 givens and determine that there is no solution. However this process could involve excessive looping and become time consuming. A quick call to this function can avoid this:
If NumberGivens(Puzzle) < 17 then
Redim Solutions(0)
Exit sub
End if
Keep in mind that calling this method will return no solution even when multiple solutions are possible. If the user is only interested in puzzle validity, then this function can dramatically speed up execution by skipping the main Do/Loop. If it is imperative to distinguish unsolvable puzzles from puzzles with multiple solutions, this function should not be implemented.
Unsolvable Puzzles
This is an invalid puzzle. The yellow cell has no possible value.
When a puzzle has one or more cells with no possible value, there is no possible solution. Brute force can detect this but this can be done more quickly with a separate function, in this case called Function PuzzleIsNotSolvable(). This is added to the code before entering the main Do/Loop.
If PuzzleIsInvalid(Puzzle)then
Redim Solutions(0) ‘value = Nothing
Exit sub
End if
|
Function PuzzleIsInvalid(ByVal Cell(,) As SByte) As Boolean
PuzzleIsInvalid = False 'invalid because one or more cells have no possible value Dim Row As Int16 Dim Col As Int16 Dim Digit As Int16
Dim HasValue As Boolean = False
For Row = 1 To 9 For Col = 1 To 9 If Cell(Row, Col) = 0 Then 'not a given HasValue = False ‘default For Digit = 1 To 9 Cell(Row, Col) = Digit ‘temporarily If HasConflict(Row, Col, Cell) = False Then HasValue = True End If Cell(Row, Col) = 0 'reset Next Digit
If HasValue = False Then 'no possible value for this cell PuzzleIsInvalid = True Exit Function End If
End If Next Col Next Row End Function
|
Naked and Hidden singles
A naked single is a cell with only one possible value. A hidden single is a cell that contains the only instance of a particular digit in a house(row, column, or box) (for example, a cell contains the only 7 in its column) . It is hidden because, unlike the naked single, it resides in a cell with other digits.
Detecting these and then treating them like givens can dramatically reduce the number of loops used in the brute force algorithm. Each time a naked or hidden single is detected and changed to a given, it can create more naked and hidden singles. For this reason, searching for singles is repeated until no more singles are detected as shown in the code below.
Many times detecting singles will be enough to solve the puzzle. When this occurs, the puzzle is proven valid before entering the main Do/Loop.
|
Do ArrayUpdated = False Call HiddenSingles(Cell, ArrayUpdated) Call NakedSingles(Cell, ArrayUpdated) Loop While ArrayUpdated
|
The Main Do/Loop
At this point, we have eliminated obviously invalid puzzles and are treating hidden and naked singles as givens. This is where the essence of the brute force algorithm performs its methods. It contains two nested loops. The outer loop moves focus to a new cell, forward or backwards. The inner loop checks all of the possible values for the current cell. The procedure ends when focus is on the first non given cell in the grid and it has no possible value. At that point, all possible solutions (hopefully only one) have been determined.
The number of times the nested loops are repeated is variable. It can be as little as a few thousand loops to hundreds of millions of loops. Intuitively one would think that the number of loops required would be related to the puzzle difficulty or the number of givens. Actually neither are true. This can be demonstrated by analyzing a puzzle using brute force, rotating the puzzle 90 degrees and retesting with brute force again. The difference in the number of loops can be very impressive.
The above puzzle was solved by brute force, requiring 12,215,690 loops and an unacceptable solving time of over 2 seconds. After rotating this puzzle 90 degrees, it required only 664,920 loops and took 0.1 seconds.
This phenomenon seems to be related to the number of blank cells early in the puzzle, that is, closest to the top left of the grid. This theory needs to be explored further to prove this but the fact remains that rotating a puzzle can dramatically affect the number of loops required to solve it.
This then is an opportunity to intervene when brute force is looping excessively. By counting the number of loops and setting an arbitrary limit, puzzle solution time can be kept to a minimum.
Experimentation so far has demonstrated that the majority of puzzles can be solved in one million loops or less. However, valid puzzles do exist that require over 50 million loops to solve. Because of this, an arbitrary limit should be set as an intervention point. One million loops requires approximately 0.2 seconds so one million is a good arbitrary limit.
So now the enhanced brute force algorithm proceeds as follows:
This code can be found in sub BruteForceEnhanced(). Each time the inner loop is executive, this code is used
|
MyCounter = MyCounter + 1 ‘inner loop counter
If MyCounter > LoopLimit Then 'rotate puzzle and retest Puzzle = RotateString(Puzzle, True) 'Rotate the cell array too Call FillCellArray(Puzzle, Cell)
RotationCounter = RotationCounter + 1
If RotationCounter = 4 Then 'back to original orientation but have ' not found a solution 'increase loop limit and try again LoopLimit = LoopLimit * 2 RotationCounter = 0 End If
MyCounter = 0 Row = 1 Col = 0 ReDim Solutions(0) SolutionCounter = 0 Exit Do End If
|
This algorithm has been tested on several hundred puzzles of varying difficulty. To date, the longest solution time for any puzzle is 0.4 seconds. The vast majority of the puzzles are solved or proven invalid in less than 0.1 seconds.
Another opportunity to improve the algorithm’s efficiency is when a solution is found. As stated previously, when a value can be placed in the last non given cell in the puzzle, a solution has been found. In order to search for another solution, the focus returns to the last non given cell and it attempts to increase its value.
In this figure, the givens are black and the solved cells are blue. The yellow cell is the last non given cell in the grid. An 8 has been successfully assigned to that cell thus completing the puzzle. The solution is stored and now the search for another solution begins. It starts with attempting to increase the value of the yellow cell.
It should be obvious that it is impossible to increment the value of the yellow cell without conflict. In fact, it is impossible to increase the value of any cell in row 9 without creating a conflict since each of these is the only remaining value in its column. The same can be said for the 3 in row 8 column 9 (above the yellow cell) as it is the only possible value in row 8.
So, when a solution is found, rather than returning to the last non given cell in the grid, the algorithm should blank all non given cells beyond row 8 column 8 and begin searching in that cell.
To continue to search for another solution, all of the yellow cells can be blanked as it is impossible to find another non conflicting value for any of those cells. Now focus is set to the 4 in row 8 column 8. It is the first cell that has the potential to be increased without causing conflict (not likely but possible).
Taking advantage of this skips a few dozen loops out of the thousands of loops required so the impact is minimal. But to maximize efficiency, a call to this subroutine is added:
Call BlankNonGivens(8,9) ‘row 8 column 9
|
Private Sub BlankNonGivens(LastRow As Int16, LastCol As Int16, ByRef Cell(,) As SByte) 'blank all non given cells starting at Cell(LastRow, LastCol) through end of puzzle Dim row As Int16 Dim col As Int16 row = LastRow col = LastCol Do If Cell(row, col) > -1 Then 'not a given, Cell(row, col) = 0 End If col = col + 1 If col > 9 Then col = 1 row = row + 1 If row > 9 Then 'done Exit Do End If End If Loop End Sub
|
The final option (so far anyway) is the option to quantitate the number of solutions when a puzzle has multiple solutions.
A call to BruteForceEnhanced has several arguments, one of which is the boolean AllSolutions. When set to FALSE, brute force will exit once a second solution has been found. When AllSolutions is set to TRUE, brute force will continue. Each solution will be placed in the Solutions() array. Since invalid puzzles can have hundreds (or millions) of solutions, an arbitrary limit of 100 solutions was added. The code presented here is part of Sub BruteForceEnhanced.
|
Call SaveSolution(NewSolution, Solutions)
If SolutionCounter > 1 Then 'multiple solutions If AllSolutions = False Then 'don't quantitate # solutions, Exit Do Else 'continue to find solutions. 'Abort if > 100 solutions If SolutionCounter > 100 Then Exit Do End If End If End If |
Running the code
If you would like to experiment with this code in vb.net, you can download BruteForce.zip which contains these three files:
modBruteForce.vb 'code module
FormCode.txt 'code for Form1.vb
sample_puzzles.txt
In Visual Studio, select File/New/Project and select:
Windows Form App (.Net framework)
The default project name is WindowsApp1.
After the new project has been created, select Form1.vb from the Solution Explorer.
Add four buttons, two text boxes, and three labels.
Use the default control name properties for the buttons and text boxes. For the buttons, change the TEXT properties to:
Button1.Text = “Brute Force”
Button2.Text = “Brute Force Enhanced”
Button3.Text = “Clear”
Button4.Text = “Rotate puzzle to right”
For the labels, rename them as (change the NAME property as well as the TEXT)
lblStatus
lblLoops
lblTime
Arrange the controls as shown below. Next double click the form to access the code (Form1.vb).
Replace all of the code with the text from FormCode.txt.
Finally, add the code module (modBruteForce.vb). To do this, go to the Solution Explorer and right click the project name (WindowsApp1). Select ADD, then select EXISTING ITEM. Navigate to where you downloaded modBruteForce.vb and select it.
Press F5 to run the project. The text file sample_puzzles.txt has several puzzles that you can copy and paste into the top text box. Experiment by clicking the BRUTE FORCE or BRUTE FORCE ENHANCED buttons and notice the difference. By using the ROTATE PUZZLE TO RIGHT, and then running either of the BRUTE FORCE routines, it shows the marked difference in solving time as the puzzle is rotated.
If you are creating your own sudoku solver/creator, feel free to incorporate modBruteForce.vb in it. If you find ways to improve it, please share it with me.
There’s always a way to build a better mousetrap but this is my approach to using brute force. As usual, feel free to share your comments, questions, criticisms, suggestions, etc. You can contact me at:
Happy coding!
John