The rules in any chain are:
- The chain must begin and end with strong links.
- There must be an odd number of links in the chain.
- All odd numbered links must be strong. Even numbered links can be either weak or strong.
(Remember that two candidates in a bivalue cell are always
strongly linked)
While an X Chain involves following just one candidate through the
chain, an XY Chain involves multiple different candidates.
When a strong link is in a bivalue cell, the candidate changes
from X to Y. The XY Chain shown below involves candidates
1,3,4,7, and 9.
In this example, the chain begins and ends with a 7. This means
at least one of the 7's (shown in blue) must exist. (It is
possible that both end of the chain are 7's since the ends cannot see
each other). 7's can be eliminated from any cell that can see
both end of the chain (r4c6 in this example).
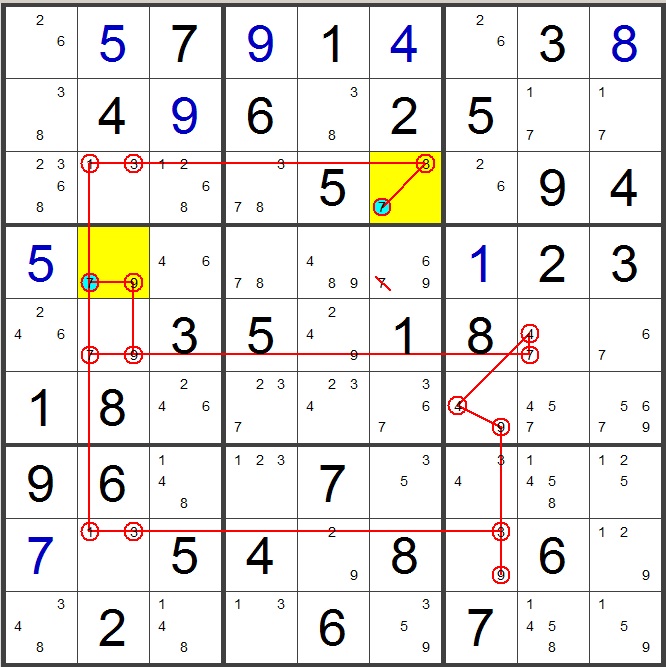 |
Chain starts with 7
1).
(r3c6)
7- 3 (strong link)
2). (r3c6 to r3c2) 3 - 3 (weak link)
3).
(r3c2)
3 - 1 (strong link)
4). (r3c2 to r8c2) 1 -1 (strong link)
5.)
(r8c2)
1 - 3 (strong link)
6). (r8c2 to (r8c7) 3 - 3 (strong link)
7.)
(r8c7)
3 - 9 (strong link)
8). (r8c7 to (r6c7) 9 - 9 (strong link)
9.).
(r6c7)
9 - 4 (strong link)
10). (r6c7 to r5c8) 4 - 4 (weak link)
11).
(r5c8)
4 - 7 (strong link)
12). (r5c8 to r5c2) 7 - 7 (weak link)
13).
(r5c2)
7 - 9 (strong link)
14). (r5c2 to r4c2) 9 - 9 (strong link)
15).
(r4c2)
9 - 7 (strong link)
Chain ends with 7
7 removed from r4c6)
|
|
|
