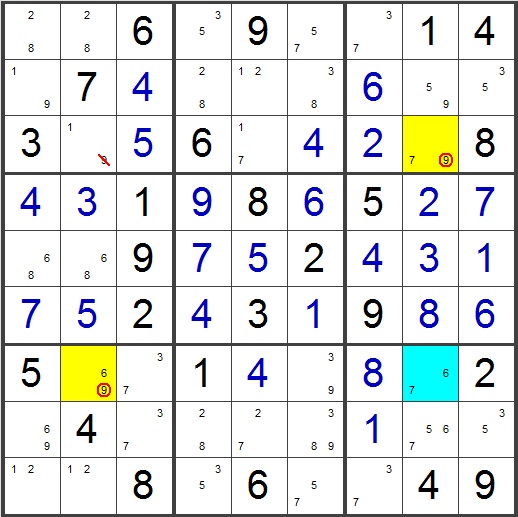
An XY-wing involves
- Three candidates
- Four cells (one base, two wings, and a target cell)
(in some cases there can be more than one target cell)
Three of these cells must be bivalue cells (except
for the target cell).
One cell is the BASE or PIVOT (shown in blue here). The next two
bivalue cells must
each be able to see the base and are called PINCERS or wings
(the yellow cells). The
final cell is the target
and must be visible to both pincers.
|
The base
(blue cell)
contains two numbers, X & Y.
(6 and 7 in this case)
The two pincers or wings must have a common candidate Z (9 in this
case).
Also one of the pincers must have an X , the other pincer
must have a Y. So pincers are the yellow cells with values
69 and 79 (XZ & YZ).
Any cell that is visible to both wings or pincers is a target cell.
The target cell
can contain any number of candidates. If the target cell contains
a Z (9 in this example), the 9 can be eliminated . (The
target cell in this example happens to be a bivalue cell but it can
contain any number of candidates).
If you look again at the blue square, whichever value it has, one of
the yellow pincers must be a 9. The target cell is visible to
both pincer cells and therefore cannot be a 9.
Another way to say this is that the 9's in the yellow cells
are now strongly linked due to their
relationship with the base.
Not all XY-wings are rectangular. Click here
for an example
(an XY-wing is also an XY-chain. Check this out)
|
|
