2 is true
2 is false
Sudoku: Understanding Chains
By John Musgrave
The concept of chains in Sudoku can be
very confusing to the reader (in my case anyway). I have read
many articles regarding chains. They are in-depth articles and
are written by authors with much more expertise than me. However,
I find much of it confusing the way the information is presented.
Sorry but I get lost by phrases like
“implication causes a contradiction,etc”. So this is my attempt (hopefully) to explain chains in a straightforward fashion.
The short explanation:
An Aternating Inference Chain (AIC) is a chain where:
As a result, the candidates at the end of the chain become strongly linked.
Alternating Inference Chain;
Got it? Cool! If not, keep reading.
The long version
Just to define some terms, a sudoku puzzle (or grid) is made up of 81 cells in 9 rows, and 9 columns (the word square is too ambiguous and should be avoided). There are also 9 boxes (9 cells arranged in a 3x3 mini grid). Three boxes arranged horizontally are called a band. Three boxes arranged vertically are called a stack. Unsolved cells contain candidates. A collection of 9 cells in a row, col, or box is called a house.
True vs False
In a cell, a candidate is said to be either true or false. When a candidate is true, the other candidates in the cell are eliminated. It also removes that candidate from related houses. When a candidate in a cell is false, it is removed from the cell.
|
|
|
|
2 is true |
2 is false |
LINKS
A chain is made up of links in the real world and in sudoku. A Link connects two candidates which are either:
The link can be either strong or weak.
A strong link exists when:
|
In a strong link, if one is false, the other must be true. Figure 1 shows a strong link between the 4’s in a box. (This is also known as a conjugate pair).
|
|
|
|
Figure 1 Strong link in a house |
|
Two candidates in a bivalue cell are also strongly linked. If one is false, the other must be true. |
|
|
|
Figure 2 Strong link in a cell |
In either of these strong links, if one candidate is true, the other must be false. But more importantly, if one candidate is false, the other must be true. This sounds very obvious but it becomes important when discussing chains.
A weak link exists between two candidates when:
|
The two circled 1’s are weakly linked. If one is true, the other must be false. However both can be false. |
|
|
|
Figure 3 Weak link |
|
Candidates 5 and 9 are weakly linked in this cell. If one is true, the other is false. However both can be false. |
|
|
|
Figure 4 Weak link in a cell |
When two candidates are weakly linked, if one is true, the other must be false (same for a strong link). However, unlike the strong link, if one is false, the status of the other digit is unknown.
Strong link: If A is true then B is false. If A is false then B is true.
Weak link: if A is true then B is false If A is false then B is uncertain.
Invalid Links
|
It is not possible to link different candidates in different cells *. Both could be true and both could be false. |
|
|
|
Figure 5 Invalid link |
* It is possible to link these candidates via an AIC. They can become strongly linked and cause some candidates elimination. More on this later.
The next step is to create a chain using these links. If the links in the chain alternate between strong and weak links, it is known as an Alternating Inference Chain (or AIC for short). When this occurs, the candidates at the ends of the chain become strongly linked. When a candidate at the end of the chain is false, the candidate at the other end of the chain must be true.
In order for an AIC to be valid, it must follow these rules:
As a result, the candidates at the ends of the AIC become strongly linked. If one is false, the other must be true. For the AIC to be relevant, it must eliminate one or more candidates from the puzzle grid. Look at figure 6.
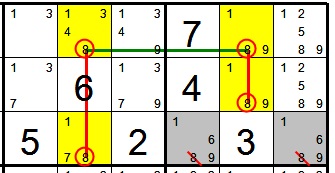
Figure 6 AIC
This is a valid AIC. It has an odd number of links (5 links). The strong links are shown in red. The weak links are shown in green. The chain begins and ends with strong links. The 8 is strongly linked to 1 in the first yellow cell. The 2nd link in the chain consists of 1’s in the column (weakly linked). The 3rd link consists of the 1’s in the row (strongly linked). The 4th link consists of the 1 and 8 that are weakly linked in a cell along with candidates 5 and 9. The 5th and final link consists of the 8’s in the column (strongly linked). As a result of the AIC, at least one of the yellow 8’s must be true. It is possible that both are true but both cannot be false.
If one end of the chain is true, we cannot conclude anything about the values in the rest of the chain. For example, if the 8 in R1C2 is TRUE, we know the 1 in R1C2 is FALSE but that’s all we know. We can’t conclude anything about the weak link in column 2 and therefore the values in the rest of the chain are unknown.
However, when the 8 is set to FALSE, it has a domino effect. Every strong link in the chain is now known (ie. we know which end of the strong link is TRUE). This ripple effect continues until it encounters the last link in the chain where the end of the chain becomes TRUE.
This is because every weak link in the chain is entered with a value of TRUE setting the other end of the weak link to FALSE. Each strong link is entered with a value of FALSE forcing the other end of the strong link to become TRUE.
As a result, we know that at least one end of the chain must be TRUE. It is possible that both ends of the chain are TRUE. However it is not possible that both ends of the chain are FALSE.
For an AIC chain to be relevant, it must eliminate one or more candidates from the puzzle. With the ends of the chain known, we are ready to use the AIC to (hopefully) eliminate one or more candidates from the puzzle grid. The candidates at the ends of the chain can be in one of the following arrangements:
The fourth possibility is two different candidates in two unrelated cells (ie. two cells that do not share a row, column, or box). In this arrangement, the AIC accomplishes nothing (see figure 6a). Either end (or both) can be true but no candidate elimination occurs.
Figure 6a Irrelevant AIC
Target Cells
In order for the AIC to be meaningful, it must cause elimination of one or more candidates. These candidates reside in target cells. Location of the target cells varies depending on the location of the chain ends and whether or not the chain ends contain the same candidate.
When an AIC begins and ends with the same candidate, there are these possible arrangements of the ends of the chain:
|
This AIC has three links. The chain ends (yellow cells) are in unrelated cells. The two potential target cells are shown in blue. They are the only cells that can see both ends of the chain. The strong links are shown as red lines. The weak link is shown in green. The slashed 5 can be removed. If none of the target cells contains a 5, the AIC is irrelevant or moot. |
|
|
When the ends of the chain (yellow) are in the same band or stack, there are six target cells (blue). In this example, only two of the target cells are relevant. |
|
|
|
Figure 7 Six target cells |
|
This AIC has 5 links. The chain ends (yellow) have created a strong link between the yellow cells. The rest of the cells in the column become target cells where candidate 2 is eliminated. |
|
Figure 9 Intersection (13 target cells)
In this AIC, the ends of the chain (yellow) reside in the intersection between a row and a box. As a result, there are 13 target cells (green). Unfortuantely, there is
only one 5 that gets eliminated.
When the ends of the chain are different candidates there are only two relevant arrangements:
Chain ends are in the same house (row, column, or box)
When the ends of the chain are different candidates in the same house, the end cells of the chain become the target cells. Neither of the candidates can exist in the other end cell of the chain. In this example, the ends of the chain (yellow cells) are candidates 6 and 8. The 8 cannot exist in the cell where the chain begins with candidate 6.
Similarly, candidate 6 cannot be present the the cell where the chain ends with candidate 8.
Figure 10 AIC with different candidates in same row
Figure 10 shows an AIC where the chain ends (candidates 6 and 8) are in the same row. The target cells are the same as the cells as the ends of the chain. If the 6 is true, it will remove the slashed 8. If the 8 is true, it will also remove the slashed 8. (If the second yellow cell contained candidate 6, it would also be eliminated).
Figure 11 AIC with different candidates in same box
Figure 11 shows another AIC where the chain ends (candidates 5 and 3) in the same house. In this case, the end cells share a box. The target cells are the same as the cells as the chain end cells. If the blue 5 is true, it will remove the slashed 5. If the yellow 3 were true, it will also remove the slashed 5.
Chain Ends In the Same Cell
The final possible AIC arrangement is where the ends of the chain are different candidates in the same cell.
Figure 12 - AIC where chain ends share same cell
Figure 12 shows an AIC where the chain begins and ends in the same cell. Candidates 1 and 5 are weakly linked in the yellow cell. However, because of the AIC, they become strongly linked. If one is false, the other must be true. In either case, the slashed 8 can be removed.
X-chains
When an AIC involves only one candidate throughout the chain, it is also referred to as an X-chain. Since it involves only one candidate, none of the links (weak or strong) can be within a cell. All links in an X-chain must be in rows, columns, or boxes.
When an X-chain has only three links, there are three possible arrangements of the links. These arrangements are more commonly known and the Skyscraper, Two String Kite, and Turbot Fish. All of them are X-chains and AIC’s.
|
|
|
|
All three strategies are X-chains with three links. The difference in the three strategies involves the orientation of the strong links (shown in red). In the Skyscraper, the strongly linked pairs are parallel while the weak link is perpendicular in a row or column. In the Two String Kite, the strongly linked pairs are perpendicular while the weak link is in a box. In the Turbot Fish, one strong link and the weak link are oriented perpendicularly while the remaining strong link is diagonally oriented in a box.
In these arrangements, the end cells of the chain are unrelated (ie. different rows, columns, and boxes). An X-chain can also create a strong link between weakly linked candidates in the same house (see figure 13).
Figure 13 X-Chain
Here is an example of how an X-chain can change a weak link to a strong link. In the column , there are five 2’s. Any two of them are weakly linked. The two yellow cells shown are the ends of the X-chain. As a result, the two yellow cells are now strongly linked. One of them must be true. Therefore, the remaining 2’s in the column can be eliminated.
XY-chains
When an AIC has its strong links within bivalue cells, it is called an XY-chain. By strict definition, an XY-chain must have all of its strong links in bivalue cells while the weak links are in houses.
|
|
|
Figure 14 - XY-chain (also an XY-wing)
Figure 14 shows an XY-chain (which is still an AIC) that begins and ends with 8 (blue cells). Since any chain must begin and end with strong links, the strong links in this example are between two candidates in bivalue cells.
Link #1 - Strong link between 8 and 9 in a bivalue cell Link #2 - Weak link between 9’s in a box Link #3 - Strong link between 9 and 3 in a bivalue cell Link #4 - Weak link between 3’s in a row Link #5 - Strong link between 3 and 8 in a bivalue cell
If either end
of the chain is false, it will force the other end to be true.
This will eliminate the 8 in the target cell (gray).
Since there are weak links in the chain, it is possible for both ends
of the chain to be true ( 8’s) but it is not possible for both ends to be false.
|
|
Figure 15 - XY-Wing (XY-chain)
Figure 15 shows another XY-chain which creates a strong link between the 1's in the blue cells. All of the strong links are inside bivalue cells. |
.
Figure 16 XY-chain (also a W-wing)
Figure 16 shows an XY-chain with five links. It similar to the XY-Wing except that:
The 1’s in the two blue cells are the ends of the chain. Since at least one of them must be true, the slashed 1’s can be eliminated. It is possible that both blue 1’s are true but they cannot both be false.
This arrangement is commonly referred to as a W-wing. W-wings are very easy to spot due the identical bivalue cells. They are also more likely to be present than XY-wings.
W-wings are often misused and can cause mistakes if used incorrectly. In figure 16, it is tempting to want to eliminate candidate 4 from the target cells. After all, If you can eliminate the 1, why not the 4? The answer is that the 1’s are the ends of the chain and become strongly linked. Not so with the 4’s. The 4’s are not strongly linked. It is possible that both of the 1’s in the blue cells are true which would make both blue 4's false. .
Now look at figure 17. What is wrong?
Figure 17
The chain in figure 17 begins and ends with strongly linked 5’s. Can you eliminate the slashed 5?
No! This chain has two links. All AIC’s must have an odd number of links.
To summarize, Alternating Inference Chains are the basis of many advanced sudoku solving strategies. Skyscrapers, Two String Kites, and Turbot Fish are all X-chains which are AIC’s. XY-wings and W-wings are XY-chains which are AIC’s.
All of the AIC’s illustrated here have 5 or fewer links. Longer AIC’s are possible provided that they still have odd numbers of links. However, longer AIC’s become impractical for traditional sudoku solving.
Figure 18 AIC with 7 links
|
|
|
Figure 19 AIC with 11 links |
|
|
|
Figure 20 AIC with 25 links |
These longer chains are interesting but impractical. Finding chains with more than five links can require thousands (or millions) of trials. They are almost certainly going to be computer generated (my hats off to any human who can find long AIC’s with pencil and paper). These are reserved for the factions who seek the ultimate in sudoku puzzle difficulty.
So the AIC is the grand daddy of them all. X-chains and XY-chains are types of AIC's and the various techniques shown are types of X-chains and XY-chains. Hopefully this makes this often confusing topic more clear.
I invite questions, comments, suggestions, criticisms, etc. Feel free to contact me at jumpindoc@gmail.com
Happy puzzling!