Sudoku: W Wings are cool!
By John Musgrave
Perhaps you’ve heard of an X Wing, XY Wing, and maybe even an XYZ Wing. They are very nice tools to use to solve those really tough puzzles. But they can be hard to spot and rare to find. Then there is the W Wing. They are much more common and easier to spot. So what is a W Wing?
A W Wing consists of:
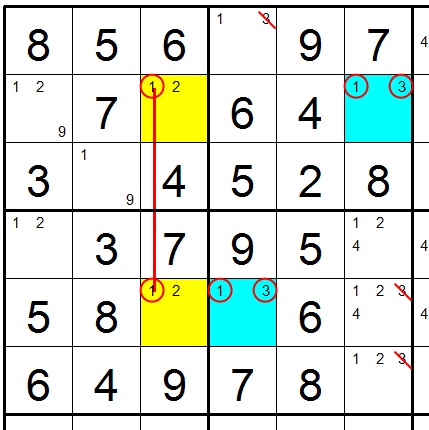
Whew! Let’s make sense out of that. Take a closer look at this puzzle:
|
We have two identical bivalue cells (13) shown in blue that cannot see each other. The next step is to find a strongly linked pair of 1’s or 3’s which can each see one of the blue cells.
The 1’s in column 3 are strongly linked (ie. there are only two of them, one must exist, the other cannot). Each of the strongly linked 1’s can see one of the blue bivalue cells. This forces at least one of the blue cells to be a 3 (but not a 1, more later).
There are four target cells that can see both of the blue cells (the slashed 3's). So now we can eliminate all of the 1’s and 3’s from the target cells, right? WRONG! Only
the 3’s can be removed. Remember the rule: if X is strongly
linked, you can eliminate Y from the target cells. In this case,
X is 1 (the strongly linked 1’s in column 3). So Y is
3. The 3’s can be removed from the target cells.
Why can’t we remove the 1’s from the target cells too? The strongly linked 1’s (yellow) force AT LEAST one of the blue cells to be a 3. The problem is that it is possible that both blue cells are 3’s. There is no link between the blue 1's. They can both be false.
In fact, that is the case in this puzzle. Both of the blue cells ARE 3’s. Check out the solution:
(Also if both the 1’s and 3’s are eliminated from the target cells, the cell at row 1 column 4 would have no possible value).
Tip: When looking for a W wing, once you find two identical bivalue cells, check the target cells first. In this example, there is only one target cell and it doesn’t contain a 3 or 9. It would be a waste to spend time searching for a matching strongly linked 3 or 9 only to find out that there is nothing to eliminate. Check your target cells first.
Here’s another example. We need to find a strongly linked 2 or 8 that can see both of the blue bivalue cells. Can you find it?
Cool! The 8’s are strongly linked in column 9 and each 8 can see one of the bivalue cells. Now which are the target cells and what candidates get eliminated?
There is only one target cell (there are actually six potential target cells but five of them are already solved). The 2 can be eliminated from the target cell but not the 8. We know that one of the blue cells must be a 2. We cannot make the same assumption about the 8. It is possible that both blue cells are 2’s (and they are in this example).
If the two blue bivalue cells share a BAND or STACK, there will be six possible target cells. Otherwise there will be only two target cells.
FYI, a W wing is actually an ALTERNATING INTERFERENCE CHAIN (or AIC). 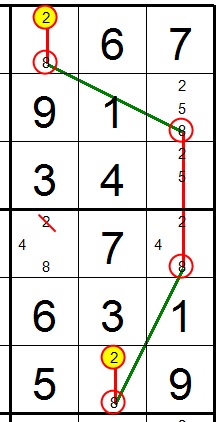 This is a chain of six candidates connected by alternating strong and weak links. As a result, the 2's at the end of the chain become strongly linked. If one is false, the other must be true. Both can be true but both cannot be false. As stated earlier, since they can both be true, the 8 cannot be removed from the target cell. This is the essence of the W wing.
So W Wings are cool because:
So now you should go out and find some W Wings. Matching pairs of bivalue cells are easy to spot. Finding a matching strongly linked pair is straight forward. Check your target cells first and be sure to keep your X’s and Y’s straight!
I invite questions, comments, suggestions, criticisms, etc. Feel free to contact me at:
Have fun!
John
|
|
|
|
|