A jellyfish is a 4 by 4 version of a swordfish (swordfish are 3 by 3)
This jellyfish is defined by the rows, eliminations occur in the
colums.
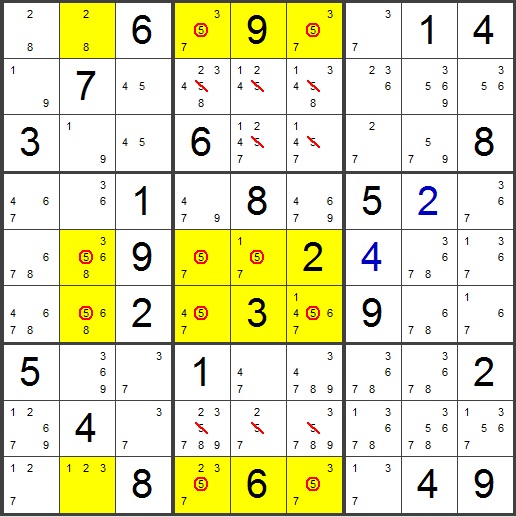 |
The sixteen yellow cells
illustrate the 4x4 nature of the Jellyfish. However, you may
notice that candidate 5 is not present in all sixteen yellow cells.
Why is this?
By definition, a Jellyfish is present when a candidate is confined to
four columns in any four rows. So when you consider the yellow
rows (1, 5, 6, & 9) , all of the 5's are confined to columns 2, 4,
5, & 6. Within those rows, there aren't any 5's outside those
columns. None of the yellow rows contain all four 5's. Rows
1 and 9 contain only two 5's. Rows 5 and 6 contain only three
5's.
In order for this to be a valid Jellyfish, a candidate must be confined
to four columns in the four selected rows. This is indeed the case
here. The important point is that the 5's must be CONFINED (but
not necessarily present in all rows) to those columns.
A 5 by 5 version of this is known as a Squirmbag.
Its another technique that you'll never need. But click the
link if you want to see one.
(back)
|
|